Programmable quantum Hall bisector: towards a novel resistance standard for quantum metrology

We experimentally demonstrate a quantum Hall (QH) architecture that allows obtaining an electrically-programmable QH resistance standard that can produce any binary fraction (k/2ⁿ) of the resistance quantum R_K/2. Remarkably, the size of the circuit only grows linearly with the integer n, and thus logarithmically with the precision of the required fraction. Every integer k value between 1 and 2ⁿ can be obtained with an easy-to-predict gate configuration and, regardless of the value of n, the circuit only requires using robust QH states at low filling factors. Finally, the device architecture does not contain any internal Ohmic contact with a net current flow, and thus it is fundamentally less susceptible than conventional arrays of QH resistance standards to errors due to spurious contact resistances. We illustrate a proof-of-principle n = 2 implementation based on a GaAs/AlGaAs heterostructure and report a relative accuracy of the output fractions of the order of 10^-4, which is at the limit of the precision currently attainable with our measurement set-up.

The basic building block of the device is depicted in Figs. 1a,b: it consists of a field-effect transistor with a set of equilibration contacts and implements a QH edge-state mixer. The device is designed to operate at a filling factor v = 2 in the ungated 2DES. The filling factor underneath the barrier region depends on the gate voltage: when the filling factor below the gate is set to v = 1, the mixer will be said to be in an active configuration; when the filling factor is v = 2, the mixer will be said to be in a neutral configuration.

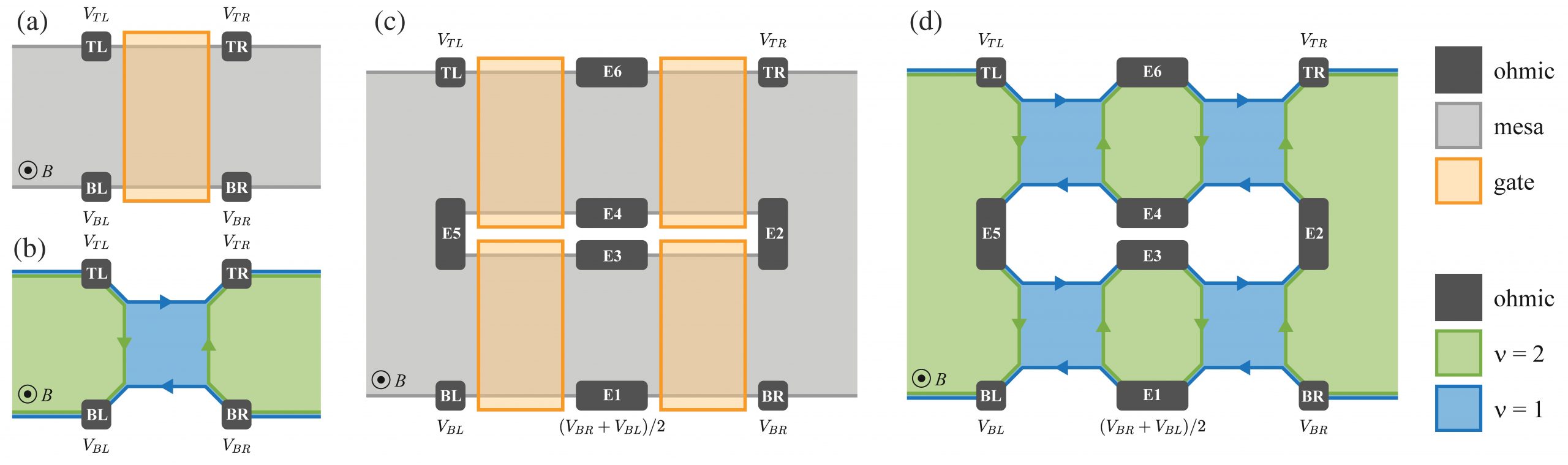
Figure 1: (a,b) Edge mixing can be obtained by patterning a single barrier on an electron gas at filling factor v = 2. The edge connectivity for the two Landau levels is visible in (b): due to edge equilibration, the top-right and bottom-left contacts both equilibrate at an average voltage V_TR = V_BL = (V_TL + V_BR)/2. (c) The action of a single mixer is fully equivalent to the double-parallel-double-serial (DPDS) mixer: this implies that any individual barrier can be replaced by a DPDS barrier without affecting the currents and potentials of the outer edge system. (d) The effect of equilibration in the DPDS mixer can be easily deduced from the edge connectivity scheme.

The operation of the mixer is straightforward. When the mixer is active, only the outer edge channel is able to cross the barrier while the inner one is completely reflected, as sketched in Fig. 1b. Given the chirality in the figure (set by the sign of the magnetic field), the Landauer-Buettiker formalism implies that the two output voltages V_TR and V_BL equilibrate to the average value of the two input voltages V_TL and V_BR, i.e.

V_TR = V_BL = (V_TL + V_BR)/2.

We note that the equilibration will naturally occur during the copropagation of edge modes and that it can be reasonably assumed to be extremely good for a macroscopic Ohmic contact. The crucial principle behind the voltage bisection scheme is the following: the single mixer in Fig. 1a is electrically equivalent to the combination of barriers and equilibration contacts visible in Fig. 1c,d which in the following will be named double-parallel-double-serial (DPDS) mixer. Here, equivalent means that any single barrier can be replaced with a DPDS barrier system without affecting in any way the voltages and the currents in the rest of the circuit. This is a basic consequence of the Landauer-Buettiker theory: once the input voltage V_TL and V_BR are set, the contacts V_TR and V_BL equilibrate at the same voltages as in the single barrier; this in turn ensures that all the input and output currents are exactly the same and thus that the two edge circuits are indistinguishable from the point of view of the rest of the QH circuit.

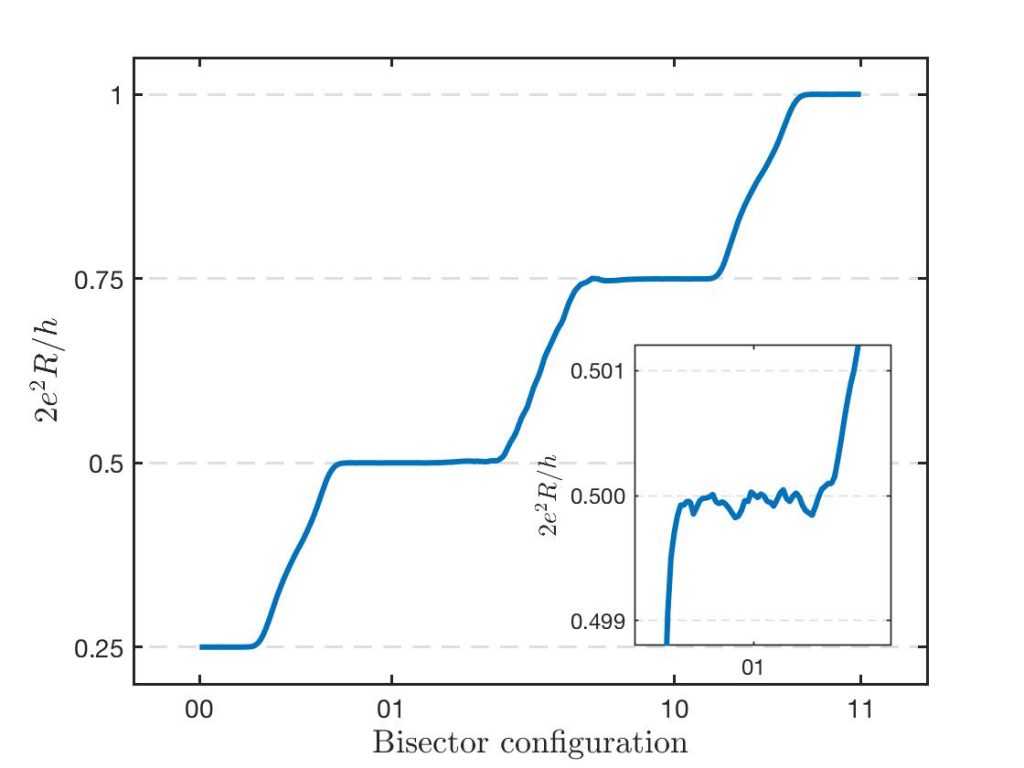
Figure 2: Experimental demonstration of a two-stage bisection circuit implementing four different quantized resistances depending on control parameters. Four plateaus are visible at the fractions 2e²R/h = 1/4, 1/2, 3/4, and 1. The precision of the quantization can be assessed from the inset showing the 0.5 plateau.

The operation of the bisection circuit is demonstrated in Fig. 2. The resulting four-wire resistance R is reported in Fig. 2 and contains clear plateaus at the predicted fractional resistance quanta. The relative quantization values are found to be consistent within a precision on the order of few parts per 10⁴, thus demonstrating the working principle.

Publications:

1. Zahra Sadre Momtaz, Stefan Heun, Giorgio Biasiol, and Stefano Roddaro: Programmable quantum Hall bisector: towards a novel resistance standard for quantum metrology, arXiv:2003.10020 [cond-mat.mes-hall].
2. Z. S. Momtaz, S. Heun, G. Biasiol, and S. Roddaro: Cascaded Quantum Hall Bisection and Applications to Quantum Metrology, Phys. Rev. Appl. 14 (2020) 024059.
3. L. Caputo: A programmable metrological standard based on the quantum Hall effect, Master thesis, University of Pisa, Italy (2020 – 2021).
4. Italian patent no. 102019000022506, title: INTEGRATED CIRCUIT CONFIGURED TO OPERATE IN THE QUANTUM HALL EFFECT REGIME FOR OBTAINING A PREDETERMINED STANDARD OF RESISTANCE [102019000022506]

Presented at:

1. L. Caputo: A programmable metrological standard based on the quantum Hall effect, Defense Talk, Master thesis, University of Pisa, Italy (May 2021).